【Python】実験屋のためのベイズ最適化入門【GPyOpt】

ベイズ最適化とは？

ベイズ最適化は、少ないデータから関数を予測する機械学習的手法で、動的実験計画法の一種です。他の機械学習とは異なり、大量のデータを必要としません。

データ間の他のデータの存在確率を見積もるガウス過程と呼ばれる手法を内部で用いており、その不確かさを埋めるように新しいデータを取っていき、関数の形を推定します。この説明に関しては、このページで試してもらう以下の最適化結果を見るとよく分かります。

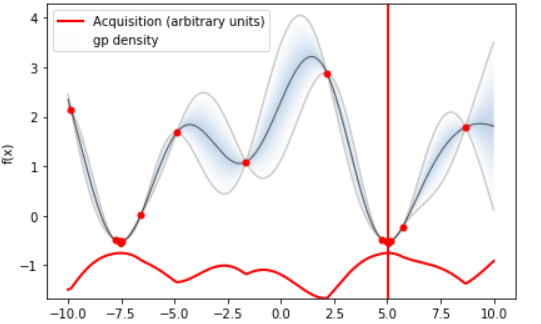
薄い青で示された領域が確率の密度を示しており、データ点同士が離れているとその間の存在確率はあいまいになります。ただ曖昧ながらも取り得るであろう値の幅（灰色で示されている弦）はガウス回帰により見積もることができるため、少ない点から全体を俯瞰して一気に最小値・最大値に詰め寄ることができるようです。

このベイズ最適化が威力を発揮するのは一回のデータ取得に非常に時間やコストがかかるタスクです。最も使われているのは機械学習のハイパーパラメータ決定（ニューロンの数や層の数：本来は人間が最初に設定する）です。機械学習は一回の学習が重いため、低いコストで最適な層数などを見積もれたら嬉しいわけです。

そして最近注目されているのが実際の実験です。物質合成には当然時間がかかり、組成提案から物性値の取得までするのに数日～数か月を要します。この組成提案と物性値の関係をベイズ最適化することで、短い期間で望ましい物性値を持つ物質を発見できます。

（面白いところでは、Googleがクッキーの美味しい作り方をベイズ最適化で研究したりしています）

必要なソフト・知識

基本的にPythonの知識が必要です。ただそれさえあれば後はライブラリが優秀なため、直感的に使うことができます。

• Python
  • Anacondaのインストール
  • ベイズ最適化ライブラリ「GPyOpt」
  • （できれば）csvやexcelをpythonで解析する技術

GPyOptのインストール

Qiitaの記事を参考にインストールを行っていく。

Anaconda promptを開き、下記コマンドを入力する。

conda update scipy
pip install GPy
pip install gpyopt

GPyOptの簡単な使い方

ここからJupyter Labを使ってGPyOptの使い方を実践していく。

まずAnaconda Prompt上で以下のコマンドを実行してJupyter Labを起動しよう。

Jupyter lab

このような画面が出れば成功。

左上の＋マークを押して、Python3を選んで新しいノートブックを作成。

GPyOptのインポート

以下のコードを一つ目のセルに入れる。

Jupyter labではセルごとにプログラムを実行していく。セルの実行は上の再生ボタンか、「Ctrl + Enter」で出来る。

import GPy
import GPyOpt
import numpy as np

実験関数の設定

実際の実験ではここで試したパラメータとその結果を入力するが、ここではsin(x)とcos(1/2x)を足し合わせた関数を作って、その値を最適化する。

def f(x):
    return np.sin(x) + np.cos(0.5*x)

このように、入力値が結果を出力するような関数を作っておく必要がある。

最適化条件の設定

以下の通り最適化の条件を設定する。

bounds = [{'name': 'x', 'type': 'continuous', 'domain': (-10,10)}]
myBopt = GPyOpt.methods.BayesianOptimization(f=f, domain=bounds,initial_design_numdata=1,acquisition_type='LCB',normalize_Y=False)

bounds(名前は何でもいい)には入力データのタイプと範囲を入力する。typeには連続値を示すcontinuousと、離散値を示すdiscreteがある。
domainには取り得る値の範囲を設定可能。ここでは-10から10までとした。

その後GPyOpt.methods.BayesianOptimization()でベイズ最適化オブジェクトを作る。作る時の引数は以下の通り

引数名	説明	選択肢
f	最適化する関数	設定した関数の名前
domain	最適化条件・制約を設定	入力の情報が入った辞書のリスト: [{},{}]など
initial_design_numdata	事前にわかっているデータの数	事前実験がない場合は0でよい
acquisition_type	獲得関数	EI,MPI,LCB
normalize_Y	出力を正規化するかどうか	True,False

特に獲得関数は様々あり、結果が変わってくるため注意が必要。
獲得関数についてはこちらのスライドが参考になる。

最適化の実行

myBopt.run_optimization(max_iter=20)

ここまで来たら、先程作ったベイズ最適化オブジェクトの.run_optimization()メソッドを呼び出せばOK.この時に、最大どれだけの実験点を取るかをmax_iter引数で設定する。今回は簡単のために20回にした。

予測結果のプロット

まずは今回の関数の形をプロットする。

from matplotlib import pyplot as plt
plt.plot(np.arange(-10,10,0.1),[f(x) for x in np.arange(-10,10,0.1)])

かなり山と谷があり、人間がこの関数上で20回値を取って最小値を見つけるのは難しいです。

ベイズ最適化した後の予測値と最小値は以下のようにして描画できます。

myBopt.plot_acquisition()

描かれている黒い線は、ベイズ最適化で得られた回帰関数。かなりの精度で入力された関数を再現していることが分かります。

赤の縦線で示されているのは最小値。無事にたった20個の点を取るだけで最小値を見つけています。

最適値の取得

print(myBopt.x_opt)
print(myBopt.fx_opt)

ベイズ最適化オブジェクトのx_optとfx_opt属性でそれぞれの値を読み取れます。

回帰関数の取得

ベイズ最適化後の平均の関数（図中の濃い青線）は以下のように取得できます。

Y = myBopt.model.model.predict(np.array(X))

Xには各列にデータ点が入ったリストが必要です。例えば0,1,2,3の場合の値を得る場合、

X = [[0],
    [1],
    [2],
    [3]]

とします。

実際の実験で使える形にする

これまでにやってきたベイズ最適化のお試しでは、最初からf(x)が決まっていました。これでは応用できませんね。

そこで、リアルな実験で使えるように改良します。ベイズ最適化シリーズ（5）　－リアルな実験で使ってみたい－を参考にしました。

少しf(x)の形を変えて、人間の入力を受け付けるようにしましょう。

#予備実験のデータ
try_ = 1
initial_x = np.array([-1, 0.5])
initial_y = np.array([1, 0.25])

initial_x = initial_x.reshape((-1,1)) #n×1の行列に変換
initial_y = initial_y.reshape((-1,1))

def f(x):
    global try_

    print("Try : " , try_ , "next x is ", x)
    score = float(input("Input y : "))

    try_ += 1

    return score

bounds = [{'name': 'a', 'type': 'continuous', 'domain': (-10,10)}]
myBopt = GPyOpt.methods.BayesianOptimization(f=f,
                                             domain=bounds,
                                             X = initial_x,
                                             Y = initial_y,
                                             normalize_Y = False,
                                             initial_design_numdata=0)
myBopt.run_optimization(max_iter=5)

print(myBopt.x_opt)
print(myBopt.fx_opt)

myBopt.plot_acquisition()

頭の中でy=x^2や他の関数を考えて、提示されたxからyを算出して入力してみてください。綺麗に結果が出るはずです。

↓頭の中でy=x^2を想像しながら5点とった場合

完全に予備実験0の場合

def f(x):
    global try_

    print("Try : " , try_ , "next x is ", x)
    score = float(input("Input y : "))

    try_ += 1

    return score

bounds = [{'name': 'a', 'type': 'continuous', 'domain': (-10,10)}]
myBopt = GPyOpt.methods.BayesianOptimization(f=f, domain=bounds,initial_design_numdata=2,acquisition_type='LCB',normalize_Y=False)
myBopt.run_optimization(max_iter=5)

initial_design_numdataを0以外にすることで、最初から入力を受け付けてくれます。この例では２回にしました。オブジェクト作成時にf(x)が2回呼び出されて、実質予備実験のようになります。

予備実験がexcelなどのデータになっている場合

書きました！「既存のExcelデータを入力としてベイズ最適化を始める【実験応用】」

参考になるリンク

• GPyOpt-sample notebook